Kako može sustav umjetne inteligencije rješavati složene matematičke probleme na razini olimpijade koristeći jasan prirodni jezik, a pritom provjeravati ispravnost vlastitog razmišljanja? DeepSeek AI je lansirao DeepSeekMath-V2, model velikog jezika s otvorenim težinama, optimiziran za dokazivanje teorema na prirodnom jeziku uz samoproveru. Ovaj model temelji se na DeepSeek-V3.2-Exp-Base, a radi kao 685B parametarska mješavina stručnjaka, dostupna na Hugging Face pod Apache 2.0 licencom.
U evaluacijama, DeepSeekMath-V2 postiže zlatne rezultate na IMO 2025 i CMO 2024, te ostvaruje 118 od 120 bodova na Putnam 2024 kada se koristi s povećanim vremenom testiranja.
Zašto nagrade za konačne odgovore nisu dovoljne?
Većina recentnih modela za matematičko razmišljanje koristi učenje s pojačanjem koje nagrađuje samo konačni odgovor na benchmark testovima poput AIME i HMMT. Ovaj pristup je doveo do značajnog napretka modela od slabih osnovnih linija do gotovo zasićenja na natjecanjima s kratkim odgovorima u roku od samo jedne godine. (Hugging Face)
Međutim, istraživački tim DeepSeek-a ističe dva strukturna problema:
- Ispravan numerički odgovor ne jamči ispravno razmišljanje. Model može doći do pravog broja kroz algebarske pogreške koje se međusobno poništavaju.
- Mnoge zadaće, poput olimpijskih dokaza i dokazivanja teorema, zahtijevaju potpun argument na prirodnom jeziku. Ove zadaće nemaju jedinstveni konačni numerički odgovor, stoga standardne nagrade za odgovore nisu primjenjive.
Stoga, DeepSeekMath-V2 optimizira kvalitetu dokaza umjesto čiste točnosti odgovora. Sustav procjenjuje je li dokaz potpun i logički ispravan, koristeći tu procjenu kao glavni signal za učenje.
Obuka verifikatora prije generatora
Osnovni dizajn je verifikator prvo. Istraživački tim DeepSeek-a obučava LLM bazirani verifikator koji može pročitati problem i kandidat dokaz, a zatim dati analizu na prirodnom jeziku i diskretnu ocjenu kvalitete u skupu {0, 0.5, 1}.
Početni podaci za učenje s pojačanjem dolaze iz Umjetnosti rješavanja problema natjecanja. Istraživački tim je prikupio 17,503 problema stiliziranih kao dokazi iz olimpijada, testova za odabir timova i post 2010. godine koji izričito zahtijevaju dokaze. Ovi problemi čine osnovni skup za hladno pokretanje RL-a. Kandidat dokazi dolaze iz modela razmišljanja DeepSeek-V3.2 koji se potiče na iterativno usavršavanje vlastitih rješenja, što povećava detaljnost, ali također stvara mnoge nesavršene dokaze. Ljudski stručnjaci označavaju ove dokaze koristeći rubricu 0, 0.5, 1, temeljeći se na rigoroznosti i potpunosti.
Verifikator se obučava pomoću Grupne relativne optimizacije politike (GRPO). Nagrada se sastoji od dva dijela:
- Nagrada za format, koja provjerava da li izlaz verifikatora slijedi fiksni predložak, uključujući odjeljak analize i konačnu ocjenu u okviru.
- Nagrada za ocjenu, koja kažnjava apsolutnu razliku između predviđene ocjene i ocjene stručnjaka.
Ova faza proizvodi verifikator koji može dosljedno ocjenjivati dokaze u stilu olimpijade.
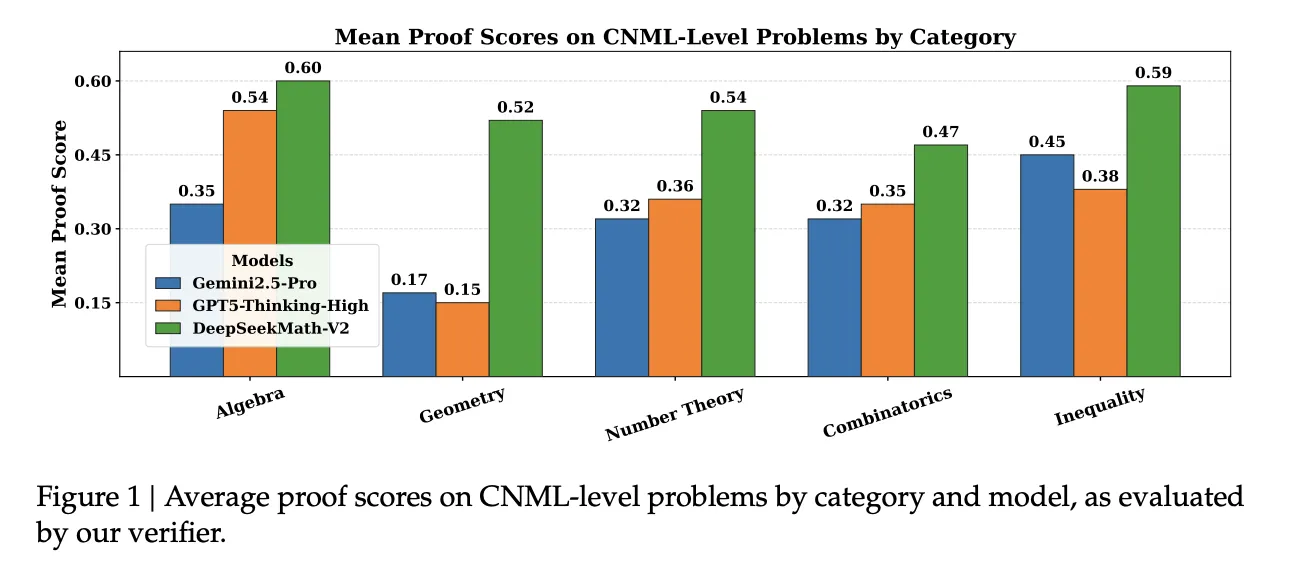
Meta verifikacija za kontrolu izmišljenih kritika
Verifikator može i dalje manipulirati nagradom. Može dati ispravnu konačnu ocjenu dok izmišlja lažne probleme u analizi. Ovo bi zadovoljilo numerički cilj, ali bi objašnjenja učinila nepouzdanima.
Kako bi se to riješilo, istraživački tim uvodi meta verifikator. Meta verifikator čita izvorni problem, dokaz i analizu verifikatora, a zatim procjenjuje je li analiza vjerna. Ocjenjuje aspekte poput ponovnog izlaganja koraka, identifikacije stvarnih nedostataka i dosljednosti između narativa i konačne ocjene.
Meta verifikator se također obučava pomoću GRPO, s vlastitim nagradama za format i ocjenu. Njegov izlaz, meta kvalitativna ocjena, koristi se kao dodatni pojam nagrade za osnovni verifikator. Analize koje izmišljaju probleme dobivaju niske meta ocjene, čak i ako je konačna ocjena dokaza ispravna. U eksperimentima, ovo povećava prosječnu meta ocjenu kvalitete analiza s oko 0.85 na 0.96 na validacijskom skupu, dok se točnost ocjena dokaza održava stabilnom.
Generator dokaza s samoproverom i sekvencijalno usavršavanje
Jednom kada je verifikator jak, istraživački tim DeepSeek-a obučava generator dokaza. Generator uzima problem i daje rješenje te samoprovalu koja slijedi istu rubricu kao verifikator.
Nagrada za generator kombinira tri signala:
- Ocjena verifikatora na generiranom dokazu.
- Suglasnost između samoprovedene ocjene i ocjene verifikatora.
- Meta verifikacijska ocjena samoprovale.
Formalno, glavna nagrada koristi težine α = 0.76…
Zaključak
DeepSeekMath-V2 predstavlja značajan napredak u području umjetne inteligencije i matematičkog dokazivanja. Ovaj model ne samo da rješava složene matematičke probleme, već također osigurava da su njegovi odgovori logički ispravni i dobro argumentirani. S obzirom na sve veći interes za primjenu AI u obrazovanju i znanosti, ovakvi modeli mogu značajno unaprijediti način na koji pristupamo učenju i rješavanju problema.
Najčešća pitanja (FAQ)
Što je DeepSeekMath-V2?
DeepSeekMath-V2 je model umjetne inteligencije optimiziran za matematičko dokazivanje na prirodnom jeziku, koji koristi samoproveru za osiguranje točnosti svojih rješenja.
Kako model provodi verifikaciju?
Model koristi verifikator koji analizira dokaze i daje ocjene temeljem rigoroznosti i potpunosti, a također uključuje i meta verifikator za dodatnu provjeru.
Koje rezultate postiže DeepSeekMath-V2?
Model postiže visoke rezultate na međunarodnim matematičkim natjecanjima, uključujući 118 od 120 bodova na Putnam 2024.
Kako se model obučava?
Obuka se provodi korištenjem podataka iz natjecanja i problema koji zahtijevaju dokaze, uz primjenu tehnika učenja s pojačanjem.
Koje su prednosti korištenja DeepSeekMath-V2?
Prednosti uključuju visoku točnost u rješavanju složenih problema, sposobnost samoprovere i generiranje logički ispravnih dokaza.
