Tehnike redukcije dimenzionalnosti poput PCA (Principal Component Analysis) izvrsno funkcioniraju kada su skupovi podataka linearno odvojivi – ali zakazuju u trenutku kada se pojave nelinearni uzorci. Upravo se to događa sa skupovima podataka poput dvaju mjeseca: PCA spljošti strukturu i pomiješa klase.
Kernel PCA ispravlja ovo ograničenje mapiranjem podataka u prostor značajki više dimenzije gdje nelinearni uzorci postaju linearno odvojivi. U ovom ćemo članku proći kroz način rada Kernel PCA i koristiti jednostavan primjer kako bismo vizualno usporedili PCA i Kernel PCA, pokazujući kako se nelinearni skup podataka koji PCA ne uspijeva odvojiti savršeno odvaja nakon primjene Kernel PCA.
Što je PCA i po čemu se razlikuje od Kernel PCA?
Analiza glavnih komponenti (PCA) je linearna tehnika redukcije dimenzionalnosti koja identificira smjerove (glavne komponente) duž kojih podaci najviše variraju. Djeluje izračunavanjem ortogonalnih linearnih kombinacija izvornih značajki i projiciranjem skupa podataka na smjerove maksimalne varijance.
Ove komponente nisu korelirane i poredane su tako da prvih nekoliko obuhvaća većinu informacija u podacima. PCA je moćan, ali dolazi s jednim važnim ograničenjem: može otkriti samo linearne odnose u podacima. Kada se primijeni na nelinearne skupove podataka — poput primjera “dva mjeseca” — često ne uspijeva razdvojiti temeljnu strukturu.
Kernel PCA proširuje PCA za rukovanje nelinearnim odnosima. Umjesto izravne primjene PCA u izvornom prostoru značajki, Kernel PCA prvo koristi funkciju jezgre (kao što je RBF, polinom ili sigmoid) za implicitnu projekciju podataka u prostor značajki više dimenzije gdje struktura nelinearnosti postaje linearno odvojiva.
PCA se zatim izvodi u ovom transformiranom prostoru pomoću matrice jezgre, bez izričitog izračunavanja projekcije više dimenzije. Ovaj “kernel trik” omogućuje Kernel PCA-u da uhvati složene obrasce koje standardni PCA ne može.
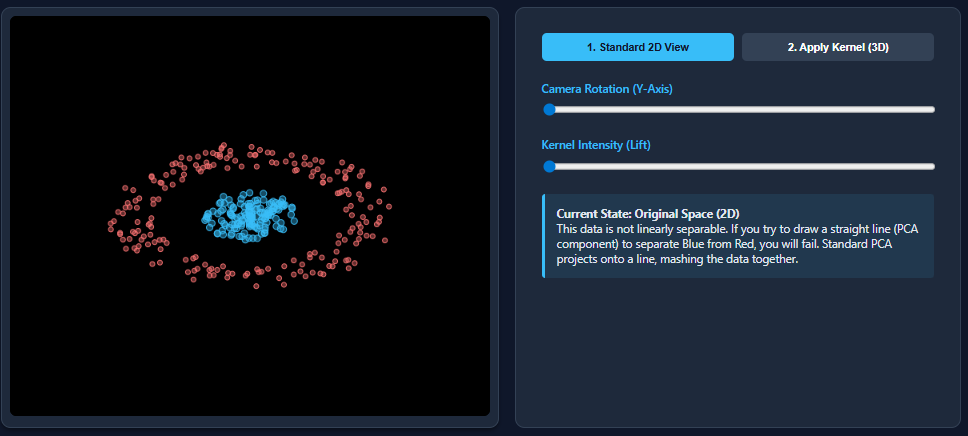

Sada ćemo kreirati skup podataka koji je nelinearan, a zatim primijeniti PCA na skup podataka.
Implementacija koda
U ovom dijelu, korak po korak, provest ćemo vas kroz implementaciju Kernel PCA koristeći Python i biblioteku Scikit-learn. Demonstrirat ćemo kako se nositi s nelinearnim skupovima podataka, konkretno s poznatim “dva mjeseca” skupom podataka. Kroz kod i vizualizacije, razumjet ćete kako Kernel PCA transformira podatke u prostor viših dimenzija kako bi omogućila bolju separaciju, dok obični PCA u tome ne uspijeva.
Generiranje skupa podataka
Generiramo nelinearni skup podataka “dva mjeseca” koristeći make_moons, koji je idealan za demonstraciju zašto PCA ne uspijeva, a Kernel PCA uspijeva.
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=1000, noise=0.02, random_state=123)
plt.scatter(X[:, 0], X[:, 1], c=y)
plt.show()
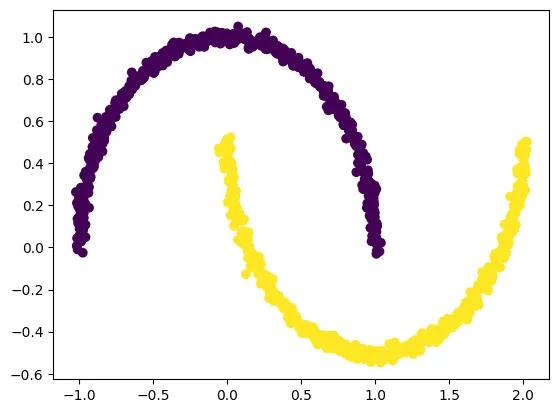
Primjena PCA na skup podataka
Sada ćemo primijeniti obični PCA na generirani skup podataka “dva mjeseca”. Kao što ćemo vidjeti, PCA neće uspjeti razdvojiti dva oblika mjeseca zbog svoje linearne prirode.
from sklearn.decomposition import PCA import matplotlib.pyplot as pltpca = PCA(n_components=2) X_pca = pca.fit_transform(X)
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=y) plt.title('PCA na skupu podataka "dva mjeseca"') plt.show()
U gornjem kodu, prvo uvozimo klasu PCA iz sklearn.decomposition. Zatim kreiramo instancu PCA modela, specificirajući broj komponenti (dimenzija) na koje želimo smanjiti podatke. U ovom slučaju, zadržavamo dvije komponente. Model se primjenjuje na skup podataka “dva mjeseca” koristeći metodu fit_transform(), koja izračunava glavne komponente i transformira podatke. Konačno, rezultati transformacije se vizualiziraju pomoću raspršenog grafikona, gdje se svaka točka boji ovisno o njenoj klasi.
Kada pokrenemo ovaj kod, vidjet ćemo da PCA nije uspjela razdvojiti dva mjeseca. Umjesto toga, dva oblika su pomiješana, što pokazuje ograničenje PCA u obradi nelinearnih podataka.
Primjena Kernel PCA na skup podataka
Sada ćemo koristiti Kernel PCA na istom skupu podataka. Kernel PCA koristi “kernel trik” za mapiranje podataka u prostor viših dimenzija, omogućujući mu da uhvati nelinearne odnose. U ovom primjeru, koristit ćemo radijalnu baznu funkciju (RBF) kernel.
from sklearn.decomposition import KernelPCA import matplotlib.pyplot as pltkpca = KernelPCA(n_components=2, kernel='rbf', gamma=15) X_kpca = kpca.fit_transform(X)
plt.scatter(X_kpca[:, 0], X_kpca[:, 1], c=y) plt.title('Kernel PCA na skupu podataka "dva mjeseca"') plt.show()
U ovom kodu, uvozimo klasu KernelPCA iz sklearn.decomposition. Kreiramo instancu Kernel PCA modela, specificirajući broj komponenti i kernel koji ćemo koristiti. U ovom slučaju, koristimo RBF kernel s parametrom gamma koji kontrolira utjecaj svakog uzorka. Primjenjujemo model na skup podataka pomoću fit_transform(). Rezultati transformacije se vizualiziraju pomoću raspršenog grafikona.
Rezultat će biti jasna separacija dvaju mjeseca, što pokazuje učinkovitost Kernel PCA u obradi nelinearnih podataka.
Ključne prednosti i nedostaci Kernel PCA
Kernel PCA, kao napredna tehnika redukcije dimenzionalnosti, nudi niz prednosti, ali dolazi i s određenim ograničenjima. Razumijevanje ovih prednosti i nedostataka ključno je za primjenu Kernel PCA u pravim situacijama.
Prednosti
- Rukovanje nelinearnim podacima: Glavna prednost Kernel PCA je sposobnost obrade nelinearnih skupova podataka. Korištenjem kernel trika, Kernel PCA mapira podatke u prostor viših dimenzija, omogućavajući mu da uhvati složene odnose koji su nevidljivi za standardni PCA.
- Fleksibilnost kernela: Kernel PCA nudi fleksibilnost u odabiru kernela. Različiti kerneli, poput RBF, polinoma ili sigmoida, mogu se koristiti za mapiranje podataka u različite prostore značajki, što omogućuje prilagodbu tehnike različitim skupovima podataka.
- Bolja separacija: U slučajevima kada je separacija podataka ključna, Kernel PCA često nadmašuje PCA. Mapiranjem podataka u prostor značajki u kojem su klase linearno odvojive, Kernel PCA može poboljšati točnost klasifikacije i klasteriranja.
- Nema eksplicitne transformacije: Kernel PCA ne zahtijeva eksplicitno izračunavanje transformacije u prostor viših dimenzija. Umjesto toga, koristi kernel funkciju za izračunavanje sličnosti između točaka podataka, što je računski učinkovitije.
Nedostaci
- Izbor kernela i parametara: Odabir pravog kernela i njegovih parametara može biti izazovan. Pogrešan odabir može dovesti do loših rezultata. Potrebno je eksperimentiranje i razumijevanje podataka.
- Računska složenost: Kernel PCA može biti računski zahtjevan, posebno za velike skupove podataka. Izračunavanje kernel matrice može biti skupo u smislu vremena i memorije.
- Interpretacija glavnih komponenti: U prostoru značajki više dimenzije, interpretacija glavnih komponenti može biti teška. Gubitak transparentnosti je potencijalni nedostatak.
- Osjetljivost na šum: Kernel PCA može biti osjetljiv na šum u podacima. Šum može utjecati na izračunavanje kernel matrice i time na rezultate.
Ukratko, Kernel PCA je moćna tehnika za redukciju dimenzionalnosti koja je idealna za nelinearne skupove podataka. Međutim, važno je uzeti u obzir prednosti i nedostatke prije primjene, te pažljivo odabrati kernel i parametre kako bi se postigli optimalni rezultati.
Usporedba PCA i Kernel PCA
Usporedba PCA i Kernel PCA ističe ključne razlike u njihovom pristupu i učinkovitosti, posebno kada se radi o nelinearnim skupovima podataka. Dok PCA radi učinkovito na linearnim podacima, Kernel PCA se ističe u obradi složenijih odnosa.
PCA (Analiza glavnih komponenti)
PCA je linearna tehnika koja se fokusira na pronalaženje glavnih komponenti, tj. smjerova u podacima s najvećom varijancom. Proces uključuje sljedeće korake:
- Izračun kovarijacijske matrice: Mjeri odnos između različitih značajki u skupu podataka.
- Izračunavanje svojstvenih vrijednosti i svojstvenih vektora: Svojstveni vektori predstavljaju glavne komponente, a svojstvene vrijednosti označavaju količinu varijance objašnjenu svakom komponentom.
- Odabir glavnih komponenti: Komponente se odabiru na temelju svojstvenih vrijednosti, s ciljem zadržavanja najvažnijih informacija uz smanjenje dimenzionalnosti.
- Projekcija podataka: Podaci se projiciraju na odabrane glavne komponente.
PCA je jednostavna i učinkovita za linearne podatke, ali ne uspijeva u slučajevima kada su odnosi nelinearni, kao što je već pokazano s primjerom “dva mjeseca”.
Kernel PCA (Kernel analiza glavnih komponenti)
Kernel PCA je nelinearna tehnika koja proširuje PCA korištenjem kernel trika. Ključni koraci uključuju:
- Mapiranje u prostor značajki: Podaci se implicitno mapiraju u prostor viših dimenzija pomoću kernel funkcije (npr., RBF, polinom).
- Izračun kernel matrice: Mjeri sličnost između svih parova točaka u prostoru značajki.
- Centriranje kernel matrice: Uklanja prosječnu vrijednost iz svakog retka i stupca matrice kako bi se osiguralo da su glavni komponente nepristrane.
- Izračun svojstvenih vrijednosti i svojstvenih vektora: Svojstveni vektori su glavne komponente u prostoru značajki.
- Projekcija podataka: Podaci se projiciraju na glavne komponente u prostoru značajki.
Kernel PCA uspijeva razdvojiti nelinearne podatke zbog transformacije u prostor viših dimenzija, što omogućava bolju separaciju. Međutim, zahtijeva pažljiv odabir kernela i parametara.
Usporedna tablica
| Značajka | PCA | Kernel PCA |
|---|---|---|
| Vrsta | Linearna | Nelinearna |
| Primjenjivost | Linearni podaci | Nelinearni podaci |
| Metoda | Izravna analiza kovarijancije | Kernel trik |
| Prostor | Izvorni prostor | Prostor značajki |
| Separacija | Loša za nelinearne podatke | Dobra za nelinearne podatke |
| Složenost | Niska | Visoka |
| Odabir parametara | Nema | Potreban je odabir kernela i parametara |
U zaključku, PCA je prikladna za jednostavne linearne skupove podataka, dok je Kernel PCA bolja za složene nelinearne podatke, ali zahtijeva dodatne korake u odabiru kernela i podešavanju parametara.
Primjene Kernel PCA u stvarnom svijetu
Kernel PCA, zbog svoje sposobnosti obrade nelinearnih podataka, nalazi široku primjenu u različitim područjima. Njegova sposobnost da identificira i analizira složene obrasce čini ga vrijednim alatom u brojnim stvarnim scenarijima.
Prepoznavanje lica
U sustavima za prepoznavanje lica, Kernel PCA se koristi za smanjenje dimenzionalnosti slika lica. Ljudska lica imaju složene nelinearne varijacije zbog različitih izraza, osvjetljenja i položaja. Kernel PCA pomaže u ekstrakciji bitnih značajki lica, smanjujući prostor značajki i poboljšavajući učinkovitost prepoznavanja. Koristi se u sustavima sigurnosti, pametnim telefonima i društvenim mrežama.
Detekcija anomalija
Kernel PCA se primjenjuje u detekciji anomalija u raznim sustavima, kao što su otkrivanje prijevara u financijama ili otkrivanje abnormalnosti u medicinskim podacima. Analizom podataka i identificiranjem odstupanja od normalnih obrazaca, Kernel PCA pomaže u identificiranju potencijalnih problema ili prijetnji. To je posebno korisno u slučajevima kada su odnosi u podacima nelinearni.
Analiza slika i videa
Kernel PCA se koristi u analizi slika i videa za smanjenje dimenzionalnosti i izdvajanje relevantnih značajki. Primjenjuje se u segmentaciji slika, prepoznavanju objekata i praćenju pokreta. Na primjer, u medicinskoj dijagnostici, Kernel PCA može pomoći u analizi medicinskih slika (npr., MRI, CT) za identifikaciju abnormalnosti.
Biometrija
U biometrijskim sustavima, Kernel PCA se primjenjuje za analizu različitih biometrijskih podataka, uključujući otiske prstiju, obrasce šarenice i obrasce glasa. Smanjenjem dimenzionalnosti i izdvajanjem ključnih značajki, poboljšava točnost i učinkovitost biometrijskih sustava za autentifikaciju i identifikaciju.
Obrada prirodnog jezika (NLP)
Iako se rjeđe koristi izravno, Kernel PCA može biti korisna u NLP-u za smanjenje dimenzionalnosti vektora riječi (word embeddings) i izdvajanje semantičkih značajki. Može pomoći u poboljšanju performansi modela za analizu teksta, klasifikaciju i generiranje teksta. Na primjer, može se koristiti za vizualizaciju odnosa između riječi.
Primjeri iz prakse
- Sigurnost: Prepoznavanje lica na aerodromima za identifikaciju sumnjivih osoba.
- Financije: Otkrivanje neobičnih transakcija i aktivnosti vezanih za prijevare.
- Zdravstvo: Analiza medicinskih slika za dijagnozu bolesti.
- Industrija: Detekcija kvarova na proizvodnim linijama.
Kernel PCA je, dakle, svestrana tehnika koja se koristi u širokom rasponu aplikacija, omogućujući učinkovitu analizu nelinearnih podataka i poboljšanje performansi u različitim područjima.
Zaključak
U ovom članku istražili smo Kernel PCA, moćnu tehniku redukcije dimenzionalnosti koja nadmašuje PCA u rukovanju nelinearnim skupovima podataka. Kroz razumijevanje osnovnih principa, implementacije i primjera iz stvarnog svijeta, stekli smo dublji uvid u njezinu funkcionalnost i primjenjivost.
Ključno je zapamtiti da Kernel PCA koristi “kernel trik” za mapiranje podataka u prostor viših dimenzija, omogućujući identificiranje složenih obrazaca koji su nevidljivi standardnom PCA. Primjer “dva mjeseca” jasno ilustrira ovu prednost.
Iako je Kernel PCA koristan, zahtijeva pažljiv odabir kernela i parametara, što može biti izazovno. No, njezina sposobnost obrade nelinearnih podataka otvara vrata brojnim primjenama u područjima poput prepoznavanja lica, detekcije anomalija, analize slika i biometrije.
Kroz temeljito razumijevanje prednosti i nedostataka Kernel PCA, čitatelji mogu donositi informirane odluke o tome kada i kako primijeniti ovu tehniku u svojim projektima i istraživanjima.
FAQ (Često postavljana pitanja)
Što je Kernel PCA?
Kernel PCA (Kernel Principal Component Analysis) je nelinearna tehnika redukcije dimenzionalnosti koja se koristi za izdvajanje glavnih komponenti iz nelinearnih skupova podataka. Koristi “kernel trik” za mapiranje podataka u prostor viših dimenzija gdje se nelinearni odnosi mogu lakše identificirati.
Koja je razlika između PCA i Kernel PCA?
PCA je linearna tehnika koja radi izravno na izvornim podacima, dok Kernel PCA koristi kernel funkciju za transformaciju podataka u prostor značajki. PCA je prikladna za linearne podatke, dok je Kernel PCA bolja za nelinearne.
Koji su primjeri kernela koji se koriste u Kernel PCA?
U Kernel PCA se često koriste različiti kerneli, uključujući:
- RBF (Radial Basis Function)
- Polinomski kernel
- Sigmoidni kernel
Kada trebam koristiti Kernel PCA umjesto PCA?
Trebali biste koristiti Kernel PCA kada radite sa skupom podataka za koji se sumnja da ima nelinearne odnose. Ako PCA ne uspijeva učinkovito smanjiti dimenzionalnost ili razdvojiti podatke, Kernel PCA može biti bolja opcija.
Kako odabrati pravi kernel i parametre za Kernel PCA?
Odabir kernela i parametara ovisi o skupu podataka. Uobičajeno je započeti s RBF kernelom i eksperimentirati s različitim parametrima (npr., gamma) kako bi se postigli najbolji rezultati. Važno je evaluirati rezultate pomoću valjanih mjera.
Koje su prednosti korištenja Kernel PCA?
Prednosti korištenja Kernel PCA uključuju sposobnost obrade nelinearnih podataka, fleksibilnost u odabiru kernela i bolju separaciju podataka u usporedbi s PCA. Također, ne zahtijeva eksplicitno izračunavanje transformacije u prostor viših dimenzija.
Koja su ograničenja Kernel PCA?
Ograničenja Kernel PCA uključuju izazove u odabiru kernela i parametara, računsku složenost, poteškoće u interpretaciji glavnih komponenti i potencijalnu osjetljivost na šum.
Gdje se Kernel PCA koristi u stvarnom svijetu?
Kernel PCA se koristi u raznim područjima, uključujući prepoznavanje lica, detekciju anomalija, analizu slika i videa, biometriju i obradu prirodnog jezika.




![ChatGPT 5 je stigao: brži, pametniji i dostupan svima [Besplatno] 8 chatgpt5](https://umjetnai.com/wp-content/uploads/2025/08/chatgpt5-360x180.webp)







